Directional Earth Fault Protection for Compensated Neutral Networks (ANSI Code 67N)

Directional earth fault protection, identified by the ANSI code 67N, is a specialized protection function used in electrical networks with a compensated neutral, typically employing a Petersen coil earthing system.

This protection is designed to detect and isolate earth faults (single-phase-to-ground faults) in such networks by distinguishing the fault current in a faulty feeder from the capacitive currents in healthy feeders. Below, I’ll explain how this protection works, its key components, and its operational principles in a clear and structured manner.

What is a Compensated Neutral Network?

A compensated neutral network is one where the neutral point of the power system (e.g., a transformer) is grounded through a Petersen coil, also known as a compensation coil. The Petersen coil is an inductor whose inductance is tuned to match the total capacitance of the network to ground.

In the event of a single-phase-to-earth fault:

The capacitive current flows from the healthy phases to ground through the network’s capacitance.
The Petersen coil provides an inductive current that ideally cancels out the capacitive current, reducing the fault current to a very small value.

However, in practice, perfect compensation is rare due to network variations or imperfect tuning, and the fault current may not be zero. To enable fault detection, a resistor is often added in parallel with the Petersen coil. This resistor introduces an active component (in-phase with the voltage) into the fault current, which is critical for the operation of the directional earth fault protection.

How Does Directional Earth Fault Protection (ANSI Code 67N) Work?

The directional earth fault protection (ANSI 67N) activates when two conditions are satisfied for a specified time delay:

The active component of the residual current exceeds a setting threshold.
- The residual current is the vector sum of the three phase currents in a feeder, typically measured using a current transformer arrangement (e.g., a core-balance CT or the sum of phase CTs).
- The “active component” is the part of the residual current that is in phase with the residual voltage (more on this below).
This active component is in the chosen detection direction.
- The detection direction is defined as the opposite direction to the residual voltage. The residual voltage is the vector sum of the three phase-to-neutral voltages, which appears during an earth fault due to the neutral point displacement.

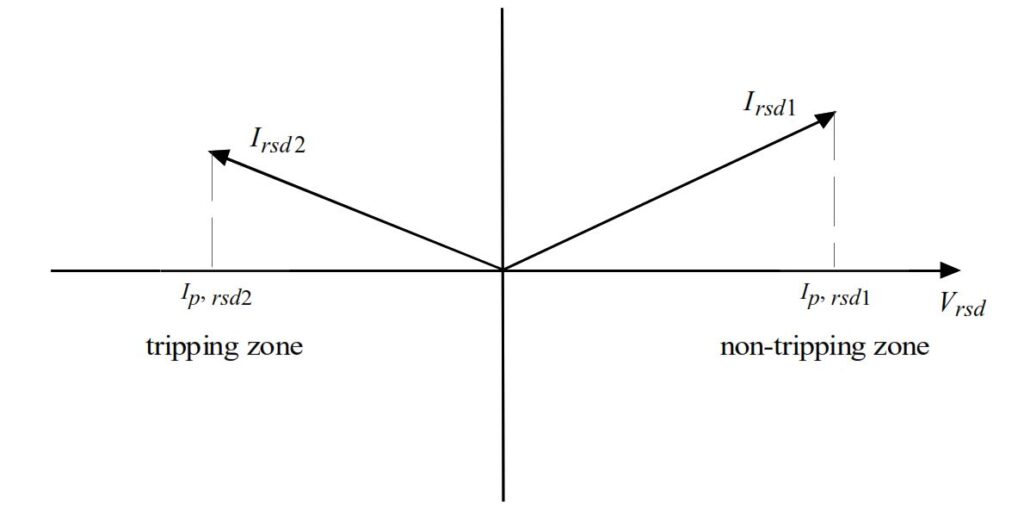
Directional earth fault protection tripping zone for a compensated neutral network

When both conditions are met, the protection identifies the feeder as faulty and initiates a trip to isolate it.

Key Concepts: Residual Current and Voltage

To understand the protection’s operation, let’s define the key electrical quantities involved:

Residual Current (I_{\text{rsd}}):
- For a faulty feeder ( $I_{\text{rsdf}}$ ): This includes contributions from the fault current (via the Petersen coil and resistor) and the capacitive currents from all feeders.
- For a healthy feeder ( $I_{\text{rsdi}}$ ): This is purely capacitive, resulting from the feeder’s capacitance to ground.
Residual Voltage (V_{\text{rsd}}):
- During a solid phase-to-earth fault, the residual voltage is approximately $V_{\text{rsd}} = -3 V_n$ , where $V_n$ is the nominal phase-to-neutral voltage. This voltage serves as a reference for determining the direction of the residual current.
Active Component:
- The active component of the residual current is its projection onto the line defined by the residual voltage. Mathematically, it’s the part of $I_{\text{rsd}}$ that aligns with $V_{\text{rsd}}$ .

Why Add a Resistor?

In a perfectly tuned compensated network (where the Petersen coil fully compensates the capacitive current), the fault current is purely reactive (90 degrees out of phase with the voltage) and lacks an active component. This makes it undetectable by standard overcurrent protection. By adding a high-value resistor in parallel with the Petersen coil:

An active current component is introduced into the fault current.
This active component is detectable and allows the directional protection to distinguish the faulty feeder.

Resistor in parallel with the Petersen coil

The resistor limits the fault current to a few amps, balancing sensitivity and safety.

In a network with a Petersen coil earthing system, the value of the earth fault current ( $I_f$ ) is given by: $I_f = j \left( 3 C \omega - \frac{1}{L_N \omega} \right) V_n$

Where:

$I_f$ : Earth fault current.
$C$ : Total network capacitance to ground.
$L_N$ : Inductance of the Petersen coil at the neutral.
$V_n$ : Nominal phase-to-neutral voltage.
$\omega$ : Angular frequency (e.g., $2\pi \times 50 \, \text{Hz}$ for a 50 Hz network).

Explanation:

The $j$ indicates the current is purely reactive in an ideal case without a parallel resistor.

The term $3 C \omega V_n$ represents the capacitive current from the healthy phases through the network’s capacitance.

The term $\frac{V_n}{L_N \omega}$ is the inductive current from the Petersen coil.

Distinguishing Faulty and Healthy Feeders

The protection relies on the difference in the residual current’s composition between faulty and healthy feeders:

Distinguishing between a fault current and a capacitive current in a compensated neutral network

Fault current $I_{\text{f}} = I_{\ell} + I_{Cf} + I_{C1} + I_{C2} + I_{C3}$

Faulty Feeder Residual Current ( $I_{\text{rsdf}}$ ):

Composed of:

An active component due to the resistor ( $\frac{V_n}{R_N}$ ).
A reactive component due to the Petersen coil and network capacitance.

Expression:

$I_{\text{rsdf}} = I_{\ell} + I_{C1} + I_{C2} + I_{C3}$

Where:

$I_{\ell} = V_n \left( \frac{1}{R_N} + \frac{1}{j L_N \omega} \right)$ (current through the neutral impedance),
$I_{Ci} = 3 j C_i \omega V_n$ (capacitive current from feeder $i$ ),
$V_n$ is the phase-to-neutral voltage,
$R_N$ is the resistor,
$L_N$ is the inductance of the Petersen coil,
$C_i$ is the capacitance of feeder $i$ ,
$\omega$ is the angular frequency (e.g., $2\pi \times 50 \, \text{Hz}$ ).

Simplified:

$I_{\text{rsdf}} = \frac{V_n}{R_N} + j \left[ 3 (C_1 + C_2 + C_3) \omega - \frac{1}{L_N \omega} \right] V_n$ Since $V_{\text{rsd}} = -3 V_n$

for a solid fault:

I_{\text{rsdf}} = -\frac{V_{\text{rsd}}}{3 R_N} - j \left[ (C_1 + C_2 + C_3) \omega - \frac{1}{3 L_N \omega} \right] V_{\text{rsd}}

If perfectly tuned ( $(C_1 + C_2 + C_3) \omega = \frac{1}{3 L_N \omega}$ ), the reactive part cancels out, leaving: $I_{\text{p,rsdf}} = -\frac{V_{\text{rsd}}}{3 R_N}$ This is purely active and aligned with $V_{\text{rsd}}$ .

2. Healthy Feeder Residual Current ( $I_{\text{rsdi}}$ ):

Purely capacitive, as it’s due only to the feeder’s capacitance: $I_{\text{rsdi}} = -I_{Ci} = -3 j C_i \omega V_n = j C_i \omega V_{\text{rsd}}$

This current is 90 degrees out of phase with $V_{\text{rsd}}$ , so its projection (active component) onto $V_{\text{rsd}}$ is zero.

3. Phase Displacement:

Faulty feeder: $I_{\text{rsdf}}$ has an active component in phase with $V_{\text{rsd}}$ (or opposite, depending on convention), due to the resistor.

Healthy feeder: $I_{\text{rsdi}}$ is perpendicular to $V_{\text{rsd}}$ , with no active component.

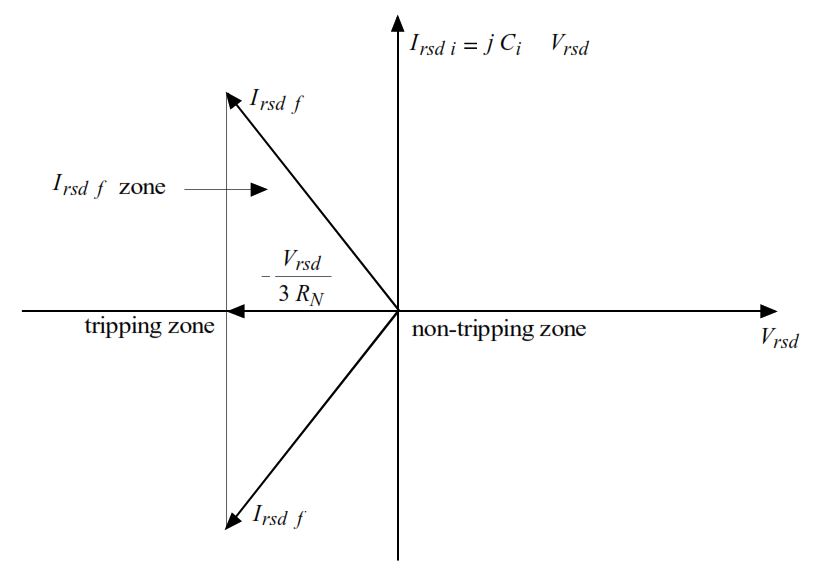
phase displacements between residual current and residual voltage detected by the healthy feeder protection and faulty feeder protection devices — Phase displacements between residual current and residual voltage detected by the healthy feeder protection and faulty feeder protection devices

Directional Detection

The protection calculates the active component by projecting $I_{\text{rsd}}$ onto $V_{\text{rsd}}$ :

For the faulty feeder: The projection is non-zero (e.g., $-\frac{V_{\text{rsd}}}{3 R_N}$ ) and in the opposite direction to $V_{\text{rsd}}$ , matching the detection criterion.
For healthy feeders: The projection is zero, so the protection does not trip.

The tripping zone, as shown in typical diagrams (e.g., Figure 7-24), defines the region where $I_{\text{rsd}}$ triggers the protection based on its magnitude and direction.

Practical Considerations

Tuning Variations: Perfect tuning is rare due to changing network conditions (e.g., capacitance variations from feeder switching). The active component persists despite mistuning, ensuring detectability.
Threshold Setting: The current threshold is set as low as possible (e.g., 1 A) to maximize sensitivity, while ensuring it exceeds the minimum detectable level of the protection device.
Selectivity: The protection ensures only the faulty feeder trips, avoiding unnecessary outages on healthy feeders. A minimum feeder length (e.g., 670 m) may be required to guarantee sufficient capacitive current for selectivity.
Why Directional? Non-directional protection might trip on healthy feeders due to capacitive currents, especially if mistuning causes $I_{\text{rsdf}}$ and $I_{\text{rsdi}}$ zones to overlap.

Conclusion

The directional earth fault protection (ANSI 67N) for compensated neutral networks operates by:

Using a resistor in parallel with the Petersen coil to introduce an active component into the fault current.
Measuring the residual current and voltage on each feeder.
Detecting the active component of the residual current (projection onto the residual voltage) and verifying its direction (opposite to $V_{\text{rsd}}$ ).
Tripping only the faulty feeder when the active component exceeds a threshold and aligns with the detection direction.

This ensures selective and reliable fault detection in compensated neutral networks, maintaining power supply continuity by isolating only the faulty feeder.